Por Der Lehrer
 |
| TEMA DEL M14 |
El LOGARITMO: CONCEPTO Y ELEMENTOS
Podemos establecer una sencilla noción del logaritmo a partir del conocimiento de una operación elemental: la exponenciación. Si bien recuerdas de lo aprendido en el M3, esta consiste en tomar un número, al cual llamamos base, y multiplicarlo por sí mismo tantas veces como nos indique otro número más pequeño colocado en la parte superior derecha: el exponente o la potencia.
Veamos un par de ejemplos:
Pensemos ahora en otra operación que nos pide determinar el exponente al que debemos elevar una base numérica para obtener otro número propuesto.
Sea:
Sea:
Si nos detenemos a calcular un poco, llegaremos con facilidad a la respuesta: el exponente buscado es el número 5, pues:
Definimos entonces al logaritmo como "el número al que debemos elevar una base númerica para obtener un número determinado." Abreviamos la operación con la palabra "log" y consideramos que :
Además, es muy importante señalar que el logaritmo solo está definido para toda base a positiva distinta de 1 (la base entonces no puede ser negativa, cero ni el número uno), y el valor de y también ha de ser siempre positivo.
Cada parte del logaritmo recibe un nombre específico:
Los siguientes ejemplos confirman la definición básica de esta operación:
Su base es, desde luego, el número 10. En ellos no se suele escribir la base, así que si te encuentras con un logaritmo sin número base, debes asumir que se trata del 10 (en caso de realizar operaciones con una cálculadora científica, trabajarás esta clase de logaritmo con la función LOG).
Ejemplo:
Definimos entonces al logaritmo como "el número al que debemos elevar una base númerica para obtener un número determinado." Abreviamos la operación con la palabra "log" y consideramos que :
Cada parte del logaritmo recibe un nombre específico:
Los siguientes ejemplos confirman la definición básica de esta operación:
¿CUÁNTOS TIPOS DE LOGARITMOS HAY?
Es posible hacer una clasificación de los logaritmos si tomamos en cuenta la base que los compone.
1. Logaritmos comunes o decimales.
Ejemplo:
Y atendiendo de nuevo a lo definido para el logaritmo, será posible llegar a los siguientes resultados sin necesidad de emplear la calculadora:
Pero ¿qué ocurre en caso de que debas calcular logaritmos decimales como los siguientes?
Log 9
Log 16
Log 240
obtendrás los siguientes resultados:
Log 240
En tal situación podrías recurrir por supuesto al uso de una calculadora científica o a tablas de logaritmos expresamente preparadas para ofrecerte los valores requeridos .
Si los resuelves vía la calculadora con la función log
obtendrás los siguientes resultados:
Log 9= 0.9542
Log 16= 1.2041
Log 243=2.3856
La característica de un logaritmo se establece por el número de posiciones que habrá que recorrer un punto decimal a partir del orden de las unidades para configurar el número del logaritmo. Si el desplazamiento es hacia la derecha, la característica será positiva; hacia la izquierda, negativa, y si no es necesario moverlo, nula o cero.
Veamos los siguientes ejemplos:
En log 4.76= 0.6776 , la característica es 0; y la mantisa 6776
En log 16= 1.2041, la característica es 1; y la mantisa 2041
En log 243= 2.3856, la característica es 2; y la mantisa 3856
En el caso de los siguientes logaritmos:
Log 0.389, la característica es -1; y la mantisa la encontraerás si ingresas log 3.89=0.5899. El resultado del logaritmo se da finalmente restando la característica a la mantisa: 0.5899-1= -0.4101
Log 0.0297, la característica es -2; la mantisa la obtienes de
log 2.97=0.4727, y el logaritmo será: 0.4727-2=-1.5272
Log 0.00452, la característica es -3; la mantisa log 4.52= 0.6551, y el total del logaritmo es 0.6551-3= -2.3449
2. Logaritmos naturales
Tienen como base al número irracional e, cuya expresión decimal es infinita (2.7182818284...). Estos logaritmos suelen anotarse con la abreviatura "ln" (así aparece la función en las calculadoras científicas).
3. Otros logaritmos
Admiten cualquier número base (recuerda que en los logaritmos solo se exceptúan los números negativos, el cero y el uno como bases) distinto a 10 o el irracional e.
LEYES Y PROPIEDADES DE LOS LOGARITMOS
Los logaritmos han sido utilizados por matemáticos y técnicos para realizar cálculos con relativa facilidad, en virtud de que cuentan con ciertas propiedades singulares que permiten la simplificación de las operaciones aritméticas.
Veamos sus atributos.
1. El logaritmo del número 1 siempre será cero, para toda base aceptada.
La razón de esta propiedad radica en una ley básica de los exponentes que ya conoces:
2. El logaritmo de la multiplicación de dos o más números equivale a la suma de los logaritmos de cada factor.
Esta propiedad puede ser deducida también de las leyes de los exponentes.
Considera los siguientes ejemplos que muestran su aplicación y examínalos.
3. El logaritmo de la división de dos números equivale a la diferencia del logaritmo del numerador y el del denominador.
También se infiere esta propiedad de las leyes de los exponentes.
Revisa los siguientes ejemplos:
4. Un logaritmo cuyo argumento tenga exponente es equivalente a un producto de este exponente por el resto de la expresión logarítmica, ya sin exponente en el argumento.
5. Un logaritmo cuyo argumento sea la raíz de índice "n" de un número, es igual a multiplicar la expresión logarítmica con argumento equivalente a la cantidad bajo la raíz, por una fracción de numerador uno y denominador igual al número del índice de dicha raíz.
Los principales logaritmos son los que poseen la base diez (decimales) y aquellos llamados naturales (base e), los cuales puedes obtener con las funciones principales de una calculadora científica. Pero ¿qué hacer si queremos calcular logaritmos de cualquier otra de las bases numéricas permitidas? Sencillo. Emplearemos otra propiedad logarítmica que nos permitirá realizar dicho cómputo
6. Para realizar el cálculo de un logaritmo en base distinta al 10 o e, se divide el logaritmo decimal del argumento entre el logaritmo decimal o natural correspondiente a la base.
A título de ejemplos podemos revisar los siguientes casos:
No lo olvides: para calcular un logaritmo de otra base puedes usar logaritmos decimales o naturales. Solo divides el logaritmo del argumento entre el logaritmo de la base (natural o decimal).
La llamada función logarítmica es una de las más importantes en la matemática, y cuenta con numerosas aplicaciones que estudiaremos más adelante.
Se trata de la función inversa de la función exponencial,lo cual suena lógico si piensas en que ambas funciones representan operaciones contrarias.
La forma general de la funcuión logarítimica es:
Los logaritmos son realmente importantes debido a que una buena cantidad de manifestaciones de la esfera natural y también de la social, puede ser expresada mediante estas herramientas matemáticas para su mejor comprensión.
Veamos algunos ejemplos.
1. GEOLOGÍA: Es muy conocida la Escala de Richter para determinar la intensidad de un sismo mediante el uso de una serie logarítmica en la que cada grado implica un orden de la base 10. Así, un terremoto de grado 8 (realmente fuerte) en esta escala vendría a ser 10 veces más potente que otro de grado 7, 100 que uno de grado 6, 1000 que otro de grado 5, y así sucesivamente...
La fórmula para determinar la intensidad de los sismos viene dada por:
R= Log (A/Ao)
2. FÍSICA: La magnitud de un sonido es cuantificada también con el empleo de una escala cuya base es el decibel (dB), unidad logarítmica que establece la relación entre la potencia de un sonido y el sonido más bajo perceptible para el hombre, ya nuestro oído humano es sensible a los sonidos siguiendo un modelo logarítmico.
B= 10 log (I/Io)dB
3. DATACIÓN DE FÓSILES Y OTROS OBJETOS: ¿Te has preguntado cómo es que los científicos pueden afirmar que algunos restos de organismos datan de periodos hace miles de años? Cuando se busca conocer la edad de algún vestigio de vida de épocas pasadas, o de rocas que forman parte de la corteza terrestre desde hace mucho tiempo, o simplemente de alguna muestra, se recurre al uso de un isótopo radiactivo del carbono, el carbono 14.
En el caso de los seres vivos, dado el hecho comprobado de que al morir un organismo comienza un proceso de desintegración en escala exponencial del carbono 14, y además se sabe el periodo que necesita la muestra para reducirse a la mitad, tan solo se requiere conocer una fórmula que relacione todos los parámetros para poder determinar con un margen mínimo de error la edad de los restos encontrados.
LA FUNCIÓN LOGARÍTMICA: GRÁFICA Y PROPIEDADES
La llamada función logarítmica es una de las más importantes en la matemática, y cuenta con numerosas aplicaciones que estudiaremos más adelante.
Se trata de la función inversa de la función exponencial,lo cual suena lógico si piensas en que ambas funciones representan operaciones contrarias.
La forma general de la funcuión logarítimica es:
Donde la base a debe ser
un número positivo distinto de 1: a>0 y a ≠ 1 .
Ahora observemos las gráficas de algunos ejemplos de función logarítmica, las cuales obtendremos fácilmente con el uso de Geogebra:
Esta es la que corresponde a la función del logaritmo común o decimal:
Y la que describe a la función del logaritmo natural:
Todas las gráficas de funciones logarítmicas poseen un conjunto de propiedades:
un número positivo distinto de 1: a>0 y a ≠ 1 .
Ahora observemos las gráficas de algunos ejemplos de función logarítmica, las cuales obtendremos fácilmente con el uso de Geogebra:
Esta es la que corresponde a la función del logaritmo común o decimal:
Y la que describe a la función del logaritmo natural:
Todas las gráficas de funciones logarítmicas poseen un conjunto de propiedades:
- Su dominio (los valores de x) comprende a todos los números reales mayores de cero x>0, por ello verás que las curvas jamás "tocarán" al eje Y
- Todas ellas cruzan al eje x en el punto (1,0), hecho que tiene sentido si recuerdas que : para todo valor admitido de la base a
- Si la base a>1, la función será creciente (la curva irá en ascenso); pero si a<1, la función será decreciente (la curva irá en descenso), como puedes comprobar en las siguientes imágenes:
LOS LOGARITMOS EN LA DESCRIPCIÓN DE FENÓMENOS NATURALES Y ALGUNOS PROCESOS SOCIALES
Los logaritmos son realmente importantes debido a que una buena cantidad de manifestaciones de la esfera natural y también de la social, puede ser expresada mediante estas herramientas matemáticas para su mejor comprensión.
Veamos algunos ejemplos.
1. GEOLOGÍA: Es muy conocida la Escala de Richter para determinar la intensidad de un sismo mediante el uso de una serie logarítmica en la que cada grado implica un orden de la base 10. Así, un terremoto de grado 8 (realmente fuerte) en esta escala vendría a ser 10 veces más potente que otro de grado 7, 100 que uno de grado 6, 1000 que otro de grado 5, y así sucesivamente...
La fórmula para determinar la intensidad de los sismos viene dada por:
R= Log (A/Ao)
2. FÍSICA: La magnitud de un sonido es cuantificada también con el empleo de una escala cuya base es el decibel (dB), unidad logarítmica que establece la relación entre la potencia de un sonido y el sonido más bajo perceptible para el hombre, ya nuestro oído humano es sensible a los sonidos siguiendo un modelo logarítmico.
B= 10 log (I/Io)dB
3. DATACIÓN DE FÓSILES Y OTROS OBJETOS: ¿Te has preguntado cómo es que los científicos pueden afirmar que algunos restos de organismos datan de periodos hace miles de años? Cuando se busca conocer la edad de algún vestigio de vida de épocas pasadas, o de rocas que forman parte de la corteza terrestre desde hace mucho tiempo, o simplemente de alguna muestra, se recurre al uso de un isótopo radiactivo del carbono, el carbono 14.
En el caso de los seres vivos, dado el hecho comprobado de que al morir un organismo comienza un proceso de desintegración en escala exponencial del carbono 14, y además se sabe el periodo que necesita la muestra para reducirse a la mitad, tan solo se requiere conocer una fórmula que relacione todos los parámetros para poder determinar con un margen mínimo de error la edad de los restos encontrados.
Dicha fórmula incluye el uso de los logaritmos y resulta en verdad una excelente herramienta para que los biólogos o historiadores puedan determinar a qué tiempo corresponde algún rastro de animal, vegetal u objeto hallado.
Donde t es el tiempo estimado de existencia del resto, T 1/2 el periodo de desintegración a la mitad del carbono 14, Nf representa la cantidad de carbono 14 presente al hallar la muestra; No es aquella que el vestigio tenía al momento de fallecer.
4. CRECIMIENTO POBLACIONAL
En otro espacio analizaremos los modelos de crecimientio para poblaciones.
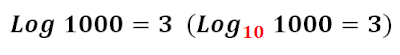
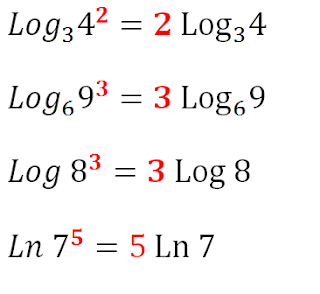
No hay comentarios.:
Publicar un comentario